MOHAMMAD YOGA FIRNANDA 126 - UMSIDA 2023
UNIVERSITAS MUHAMMADIYAH SIDOARJO
MATERI MODUL
POKOK BAHASAN 1
STRUKTUR DATA, ARRAY, POINTER, DAN STRUKTUR
PENDAHULUAN
Pada pokok bahasan ini berisi penjelasan disertai contoh mengenai konsep struktur data, array, pointer, dan struktur yang menjadi pemahaman dasar bagi mahasiswa sebelum mempelajari struktur data, di mana konsep array, pointer, dan struktur digunakan untuk merepresentasikan sebuah struktur data, diharapkan mahasiswa dapat :
a. Mengetahui konsep dasar struktur data.
b. Memahami konsep array, pointer, dan struktur.
PENYAJIAN (TUTORIAL)
A. Konsep Dasar Struktur Data
Struktur data adalah sebuah bagian dari ilmu pemrograman dasar yang mempunyai karakteristik yang terkait dengan sifat dan cara penyimpanan sekaligus penggunaan atau pengaksesan data.
Struktur data bertujuan agar cara mempresentasikan data dalam membuat program dapat dilakukan secara efisien dalam pengolahan di memori dan pengelolahan penyimpanan dari program ke storage juga lebih muda dilakukan.
B. Konsep Dasar Array
Array adalah kumpulan elemen-elemen data. Kumpulan elemen tersebut mempunyai susunan tertentu yang di teratur. Jumlah elemen terbatas, dan semua elemen mempunyai tipe data yang sama. Jenis-jenis array :
Array Satu Dimensi
Struktur array satu dimensi dapat dideklarasikan dengan bentuk
Umum berupa : tipe_var nama_var [ukuran];
Dengan ;
- Tipe_var : untuk menyatakan jenis elemen array (misalnya int, char, unsigned).
- Nama_var : untuk menyatakan nama variable yang di pakai.
- Ukuran : untuk menyatakan jumlah maksimal elemen array.
Contoh : float nilai_ujian [5];
Array Dua Dimensi
Tipe data array dua dimensi bisa digunakan untuk menyimpan mengolah maupun menampilkan suatu data dalam bentuk table atau matriks. Untuk mendeklarasikan array agar dapat menyimpan data adalah :
Ripe_var nama_var [ukuran1][ukuran2];
Dimana :
- Ukuran1 menunjukkan jumlah/nomor baris.
- Ukuran2 menunjukkan jumlah/nomor kolom.
Jumlah elemen yang dimiliki array dua dimensi dapat ditentukan dari hasil
perkalian :
ukuran1 x ukuran2.
Seperti halnya pada array satu dimensi, data array dua dimensi akan ditempatkan pada memori secara brurutan.
Array Multidimensi / Dimensi Banyak
Array berdimensi banyak atau mulidimensi terdiri dari array yang tidak terbatas hanya dua dimensi saja. Bentuk umum pendeklarasian array
multidimensi adalah : tipe_var nama_var [ukuran1][ukuran2]…[ukuran];
contoh : int data_angka[3][6][6];
Yang merupakan array tiga dimensi.
Mengakses Elemen Array:
Dalam Bahasa C++, data array akan disimpan dalam memory pada alokasi yang berurutan.
Elemen pertama biasanya mempunyai indeks bernilai 0. Contoh :
Float nilai_tes[5];
Jika pada contoh di atas, variable nilai_tes mempunyai 5 elemen, maka elemen pertama mempunyai indeks sama dengan 0, elemen kedua mempunyai indeks 1, dan seterusnya. Bentuk umum pengaksesan suatu elemen variable array adalah :
Nama_var[indeks];
Gambar berikut memperlihatkan urutan komponen array memori.
Untuk variable array nilai_tes :
Gambar 1.1 Struktur Array Satu Dimensi
Inisialisasi Array :
Array dapat diinisialisasikan secara langsung saat pertama kali dideklarasikan (efisien
untuk array berdimensi sedikit).
Contoh : int x[2]={1,2};
Array dapat dideklarasikan terlebih dahulu, baru kemudian diisi elemennya.
Contoh :
Int x[2];
X[0]=1;
X[1]=2;
C. Konsep Dasar Pointer
Pointer adalah sebuah variable yang berisi lamat variable yang lain. Suatu pointer dimaksudkan untuk menunjuk ke suatu alamat memori sehingga alamat dari suatu variable dapat diketahui dengan mudah. Deklarasi pointer :
Operator pointer :
Operator ‘&’ : untuk mendapatkan alamat memori operand/ variabel.
pointer ‘*’ : untuk mengakses nilai data operand/ variable pointer.
D. Konsep Dasar Struktur
Struktur adalah koleksi dari variabel yang dinyatakan dengan sebuah nama, dengan sifat setiap variabel dapat memiliki tipe yang berlainan. Struktur biasa dipakai untuk mengelompokkan beberapa informasi yang berkaitan menjadi sebuah satu kesatuan. Contoh sebuah struktur adalah informasi data tanggal, yang berisi tanggal, bulan, dan tahun.
Mendeklarasikan Struktur :
Contoh pendefinisian tipe data
Struktur adalah : struct
Data_tanggal
{int tanggal;
Masing-masing tipe dari elemen struktur dapat berlainan. Adapun variable_struktur1 sampai dengan variabel_struktur M menyatakan bahwa variable struktur yang dideklarasikan bisa lebih dari satu jika ada lebih dari satu variable, antara variabel struktur dipisahkan dengan tanda koma.
Mengakses Elemen Struktur :
Elemen dari struktur dapat diakses dengan menggunakan bentuk :
Variabel_struktur.nama_field
Antara variabel_struktur dan nama_field dipisahkan dengan operator titik
(disebut operator anggota struktur). Contoh berikut merupakan instruksi
Tgl_lahir.tang
Gal=30 int
Bulan;
Int tahun;
}
Yang mendefinisikan tipe struktur Bernama data_tanggal, yang terdiri dari tiga buah elemen berupa tanggal, bulan, dan tahun. Bentuk umum dalam mendefinisikan dan mendeklarasikan struktur adalah :
Struct nama_tipe_struktur
{
Tipe
Field1
; Tipe
Field2
; Tipe
Field3
;
}variabel_struktur1…. variabel_strukturM;
POKOK BAHASAN 2
LINKED LIST (SENARAI)
PENDAHULUAN
Pada pokok bahasan ini akan dibahas mengenai struktur data senarai (list) yang pembahasannya meliputi definisi dan representasi list, jenis-jenis list serta oerasi-operasi dasar pada list. Sehingga setelah mempelajari bab ini diharapkan mahasiswa mampu :
a. Menjelaskan definisi dan representasi list.
b. Mengetahui jenis-jenis list.
c. Memahami operasi-operasi pada list.
PENYAJIAN (TUTORIAL)
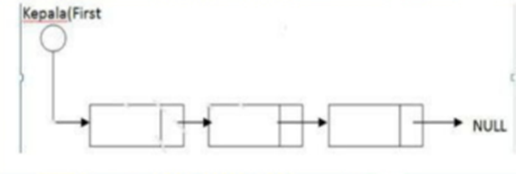
Linked list adalah sejumlah objek atau elemen yang dihubungkan satu dengan lainnya sehingga membentuk suatu list. Sedangkan objek atau elemen itu sendiri adalah merupakan gabungan beberapa data (variabel) yang dijadikan satu kelompok atau structure atau record yang dibentuk dengan perintah struct. Untuk menggabungkan objek satu dengan lainnya, diperlukan paling tidak sebuah variabel yang bertipe pointer. Syarat linked list adalah harus dapat diketahui alamat simpul pertama atau biasa dipakai variabel First/Start/Header. Struktur dasar sebuah list seperti gambar berikut :
Gambar 2.1 List Tunggal
Istilah – istilah dalam linked list :
- Simpul
Simpul terdiri dari dua bagian yaitu :
a. Bagian data
b. Bagian pointer yang menunjuk ke simpul berikutnya
- First/Header
Variabel First/Header berisi alamat (pointer)/ acuan (reference) yang menunjuk lokasi simpul pertama linked list, digunakan sebagai awal penelusuran linked list.
- Nil/Null
Tidak bernilai, digunakan untuk menyatakan tidak mengacu ke mana pun.
- Simpul Terakhir (Last)
Simpul terakhir linked list berari tidak menunjuk simpul berikutnya. Tidak terdapat alamat disimpan di field pointer (bagian kedua dari simpul). Nilai null atau nil disimpan di field pointer di simpul terakhir.
Jenis – jenis linked list :
List kosong
List kosong hanya terdiri dari sebuah petunjuk elemen yang berisi NULL (kosong), tidak memiliki satu buah elemen pun sehingga hanya berupa penunjuk awal elemen berisi NULL.
List Tunggal
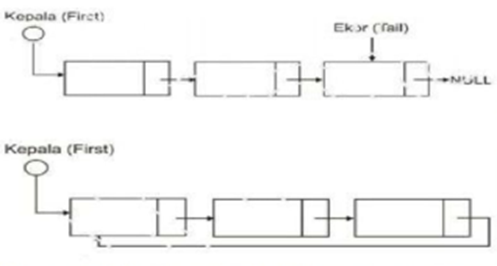
List tunggal adalah list yang elemennya hanya menyimpan informasi elemen setelahnya (next), sehingga jalanya pengaksesan list hanya dapat dilakukan secara maju. List tunggal terbagi menjadi tiga jenis yaitu list tunggal dengan kepala (first), list tunggal kepala (first) dan ekor (tail), serta list tunggal yang berputar.
Gambar 2.2 List Tunggal dengan Kepala dan Ekor, List Tunggal Berputar
List Ganda
List ganda adalah sebuah list yang elemennya menyimpan informasi elemen sebelumnya dan informasi elemen setelahnya, sehingga proses penelusuran list dapat dilakukan secara maju dan mundur. List ganda terbagi menjadi tiga jenis yaitu list ganda dengan kepala (first), list ganda dengan kepala (first) dan ekor (tail), serta list ganda yang berputar.
Gambar 2.3 List ganda dengan Kepala, List ganda dengan Kepala dan Ekor
Operasi Dasar pada Linked List :
IsEmpty : Fungsi ini menentukan apakah linked list kosong atau tidak.
Size : operasi untuk mengirim jumlah elemen di linked list.
Create : operasi untuk penciptaan list baru yang kosong.
Insertfirst : operasi penyisipan simpul sebagai simpul pertama.
Insertafter : operasi untuk penyisipan simpul setelah simpul tertentu.
Insertlast : operasi untuk penyisipan simpul sebagai simpul terakhir.
Insertbefore : operasi untuk penyisipan simpul sebelum simpul tertentu.
Deletefirst : operasi penghapusan simpul pertama.
Deleteafter : operasi penghapusan setelah simpul tertentu.
Deletelast : operasi penghapusan simpul terakhir.
POKOK BAHASAN 3
STACK (TUMPUKAN)
PENDAHULUAN
Pada pokok bahasan ini akan dibahas mengenai struktur data tumpukan atau stack, di mana stack merupakan suatu kumpulan data yang seolah-olah ada data yang diletakkan di atas data yang lain. Setelah mempelajari materi ini diharapkan mahasiswa mampu untuk :
a. Mengetahui dan memahami definisi stack.
b. Memahami operasi-operasi dasar stack.
c. Memahami representasi statis dan dinamis stack.
PENYAJIAN (TUTORIAL)
Stack adalah kumpulan elemen-elemen yang tersimpan dalam suatu tumpukan. Aturan penyisipan dan penghapusan elemennya tertentu :
- Penyisipan selalu dilakukan “di atas “ TOP
- Penghapusan selalu dilakukan pada TOP
Karena aturan penyisipan dan penghapusan semacam itu, TOP adalah satu-satunya alamat tempat terjadi operasi, elemen yang ditambahkan paling akhir akan menjadi elemen yang akan dihapus. Dikatakan bahwa elemen Stack tersusun secara LIFO (Last In First Out).
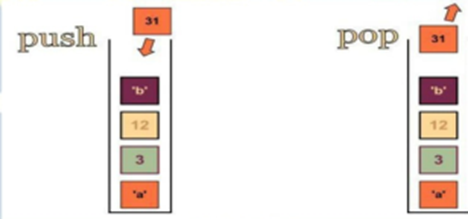
Seperti halnya jika kita mempunyai sebuah tumpukan buku, agar tumpukan buku itu tidak ambruk ketika kita mengambil sebuah buku di dalam tumpukan itu maka harus diambil satu per satu dari tumpukan yang paling atas dari tumpukan.
Gambar 3.1 Ilustrasi Stack
Perhatikan bahwa dengan definisi semacam ini, representasi tabel sangat tepat untuk mewakili stack, karena operasi penambahan dan pengurangan hanya dilakukan disalah satu ujung tabel.
Beberapa contoh penggunaan stack adalah pemanggilan prosedur, perhitungan ekspresi aritmatika, rekursifitas, backtracking, peganan interupsi, dan lain-lain. Karakteristik penting stack sebagai berikut :
1. Elemen stack yaitu item-item data di elemen stack
2. TOP (elemen puncak dari stack)
3. Jumlah elemen pada stack
4. Status/kondisi stack, yaitu :
- Penuh
Bila elemen di tumpukan mencapai kapasitas maksimum tumpukan. Pada kondisi ini, tidak mungkin dilakukan penambahan ke tumpukan.Penambahan di elemen menyebabakan kondisi kesalahan Overflow.
- Bila tidak ada elemen tumpukan. Pada kondisi ini, tidak mungkin dilakukan pengambilan elemen tumpukan. Pengambilan elemen menyebabkan kondisi kesalahan Underflow.
Stack memiliki operasi-operasi pokok sebagai berikut :
Push : Untuk menambahkan item pada tumpukan paling atas.
void Push (itemType x, Stack*S)
{
If(Full (S))
Printf(“Stack FULL”);
else
{
S->item[S->Count]=x;
++(S->count);
}
}
Pop : Untuk mengambil item teratas.
int Pop (Stack S, itemType x)
{
if (Empty (S))
Printf(“Stack Kosong”);
else
{
-(S->Count);
x=s->item(s->Count);
}
}
Clear : Untuk mengosongkan stack.
void InitializeStack (Stack S)
{
S->Count=0;
}
IsEmpty : Untuk memerikasa apakah stack kosong.
int Empty (Stack *S)
{
return (S->Count==0);
}
IsFull : Untuk memeriksa apakah stack sudah penuh.
int Full (Stack S)
{
return(S->Count==MAXSTACK);
}
Representasi stack :
- Representasi statis
Stack dengan representasi statis biasanya diinplementasikan dengan menggunakan array. Sebuah array memiliki tempat yang dialokasikan diawal sehingga sebuah elemen yang dimasukan dalam sebuah array terbatas pada tempat yang ada pada array. Karena menggunakan array maka stack dengan representasi statis dalam mengalami kondisi elemen penuh. Ilustrasi stack dengan representasi statis dapat dilihat pada gambar 3.2 :
Gambar 3.2 Representasi Stack Statis
- Representasi dinamis
Stack dengan representasi dinamis biasanya diimplementasikan dengan menggunakan pointer yang menunjuk pada elemen-elemen yang dialokasikan pada memori. Ilustrasi stack dengan representasi dinamis dapat dilihat pada gambar 3.3 :
Gambar 3.3 Representasi Stack Dinamis
Karena semua operasi pada sebuah stack diawali dengan elemen yang paling atas maka jika menggunakan representasi dinamis saat elemen ditambahkan akan menggunakan penambahan elemen pada awal stack (addfirst) dan saat pengambilan atau penghapusan elemen menggunakan penghapusan di awal stack (delfirst).
POKOK BAHASAN 4
QUEUE (ANTRIAN)
PENDAHULUAN
Pada pokok bahasan ini akan di bahas mengenai antrian atau queue, di mana struktur data ini hamper sama dengan tumpukan atau stack yang merupakan struktur data yang linier. Perbedaannya adalah pada operasi penambahan dan pengurangan pada ujung yang berbeda. Setelah mempelajari materi ini diharapkan mahasiswa mampu:
a. Mengetahui dan memahami definisi antian.
b. Memahami operasi-operasi dasar pada antrian.
c. Memahami representasi statis dan dinamis pada antrian.
PENYAJIAN (TUTORIAL)
Antrian adalah salah satu kumpulan data yang penambahan elemennya hanya bisa dilakukan pada suatu ujung (disebut sisi belakang atau REAR), dan penghapusan atau pengambilan elemen dilakukan lewat ujung yang lain (disebut sisi depan atau FRONT). Prinsip yang digunakan dalam antrian ini adalah FIFO (First In First Out) yaitu elemen yang pertama kali masuk akan keluar pertama kalinya.
Penggunaan antrian antara lain simulasi antrian di dunia nyata (antrian pembelian tiket), sistem jaringan komputer (pemrosesan banyak paket yang datang dari banyak koneksi pada suatu host, bridge, gateway), dan lain-lain.
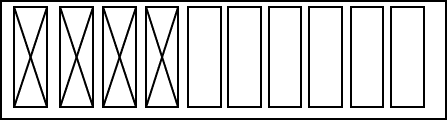
Gambar 4.1 Ilustrasi Antrian dengan 8 elemen
Karakteristik penting antrian sebagai berikut:
a. Elemen antrian yaitu item-item data terdapat dalam antrian.
b. Head/front (elemen terdepan antrian).
c. Tail/rear (elemen terakhir antrian).
d. Jumlah antrian pada antrian (count).
e. Status/kondisi antrian, ada dua yaitu:
- Penuh
Bila elemen pada antrian mencapai kapasitas maksimum antrian. Pada kondisi ini, tidak mungkin dilakukan penambahan ke antrian. Penambahan di elemen menyebabkan kondisi kesalahan Overflow.
-Kosong
Bila tidak ada elemen antrian. Pada kondisi ini, tidak mungkin dilakukan pengambilan elemen antrian. Pengambilan elemen menyebabkan kondisi kesalahan Underflow.
Operasi-operasi pokok pada antrian diantaranya adalah:
1. Create → Membuat antrian baru.
NOEL(CREATE(Q)) = 0
FRONT(CREATE(Q)) = tidak terdefinisi
REAR(CREATE(Q)) = tidak terdefinisi
2. IsEmpety → Untuk memeriksa apakah Antrian sudah penuh atau belum.
ISEMPETY(Q) = True, jika Q adalah queue kosong.
3. IsFull→ Mengecek apakah Antrian sudah penuh atau belum.
ISFULL(Q) = True, jika Q adalah queue penuh.
4. Enqueue/Insert → menambahkan elemen ke dalam Antrian, penambahan elemen selalu ditambahkan di elemen paling belakang.
REAR(INSERT(A,Q)) =A
ISEMPETY (INSERT(A,Q)) = FALSE
Algoritma QINSERT :
a. IF FRONT = 1 AND REAR = N, OR IF FRONT = REAR + 1, THEN OVERFLOW, RETUN
b. IF FRONT := NULL, THEN
SET FRONT := 1 AND REAR := 1
ELSE IF REAR = N, THEN
SET REAR := 1
ELSE
SET REAR := REAR+1
c. SET QUEUE[REAR] := ITEM
d. RETURN
1. Dequeue/Remove → untuk menghapus elemen terdepan/pertama dari Antrian
Algoritma QDELETE:
a. IF FRONT := NULL, THEN UNDERFLOW, RETURN
b. SET ITEM := QUEUE[FRONT]
c. [FIND NEW VALUE OF FRONT]
IF FRONT = REAR, THEN
SET FRONT = REAR, THEN SET FRONT := NULL AND REAR : NULL
ELSE IF FRONT = N, THEN
SET FRONT =1
ELSE
SET FRONT := FRONT+1
d. RETURN
Representasi queue :
· Representasi statis
Queue dengan representasi statis biasasnya diimplementasikan dengan menngunakan array. Sebuah array memiliki tempat yang di alokasikan diawal sehingga sebuah elemen yang dimasukkan dalam sebuah array terbatas pada tempat yang ada pada array. Karena menggunakan array maka queue dengan representasi statis dalam mengalami kondisi elemen penuh. Ilustrasi queue dengan representasi statis dapat dilihat pada gambar:
10 9 8 7 6 5 4 3 2 1 Indexs
Gambar 4.2 Representasi Queue Statis
· Representasi dinamis
Queue dengan representasi dinamis biasanya diimplementasikan dengan menggunakan pointer yang menunjuk pada elemen –elemen yang dialokasikan pada memori. Ilustrasi queue representasi dinamis dapat dilihat pada gambar :
Gambar 4.3 Representasi Queue Dinamis
POKOK BAHASAN 5
REKURSIF
PENDAHULUAN
Pada pokok bahasan ini akan dibahas mengenai rekursif. Setelah mempelajari bab ini diharapkan mahasiswa mampu:
a. Mengetahui dan memahami defenisi rekursif.
b. Memahami sifat-sifat rekursif.
c. Mengaplikasikan rekursif.
PENYAJIAN (TUTORIAL)
Fungsi rekursif adalah suatu fungsi yang memanggil dirinya sendiri, artinya fungsi tersebut dipanggil di dalam tubuh fungsi itu sendiri. Contoh menghitung nilai faktorial. Rekursif sangat memudahkan untuk memecahkan permasalahan yang kompleks. Sifat-sifat rekursif:
· Dapat digunakan ketika inti dari masalah terjadi berulang kali.
· Sedikit lebih efisien dari iterasi tapi lebih elegan.
· Method-methodnya dimungkinkan untuk memanggil dirinya sendiri.
Data yang berada dalam method tersebut seperti argument disimpan sementara ke dalam stack sampai method pemanggilnya diselesaikan.
POKOK BAHASAN 6
SORTING (PENGURUTAN)
PENDAHULUAN
Setelah mempelajari bab ini diharapkan mahasiswa mampu:
a. Menunjukkan beberapa algoritma dalam pengurutan.
b. Menunjukkan bahwa pengurutan merupakan suatu persoalan yang bisa diselesaikan dengan sejumlah algoritma yang berbeda satu sama lain.
c. Dapat memilih algoritma yang paling sesuai untuk menyelesaikan suatu permasalahan pemrograman.
PENYAJIAN (TUTORIAL)
Pengurutan data (sorting) didefinisikan sebagai suatu proses untuk menyusun kembali himpunan obyek menggunakan aturan tertentu. Ada dua macam urutan yang biasa digunakan dalam proses pengurutan yaitu:
· Urutan naik (ascending) yaitu dari data yang mempunyai nilai paling kecil sampai paling besar.
· Urutan turun (descending) yaitu dari data yang mempunyai nilai paling besar sampai paling kecil.
Contoh : data bilangan 5, 2, 6, dan 4 dapat diurutkan naik menjadi 2, 4, 5, 6 atau diurutkan turun menjadi 6, 5, 4, 2. Pada data yang bertipe char, nilai data dikatakan lebih kecil atau lebih besar dari yang lain didasarkan pada urutan relatif (collating sequence) seperti dinyatakan dalam tabel ASCII. Keuntungan dari data yang sudah dalam keadaan terurut yaitu :
· Data mudah dicari, mudah untuk dibetulkan, dihapus, disisipi atau digabungkan. Dalam keadaan terurutkan, kita mudah melakukan pengecekan apakah ada data yang hilang. Misalnya kamus bahasa, buku telepon.
· Mempercepat proses pencarian data yang harus dilakukan berulang kali.
Beberapa faktor yang berpengaruh pada efektifitas suatu algoritma pengurutan antara lain:
· Banyak data yang diurutkan.
· Kapasitas pengingat apakah mampu menyimpan semua data yang kita miliki.
· Tempat penyimpanan data, misalnya piringan ,pita atau kartu, dll.
Beberapa algoritma metode pengurutan dan prosedurnya sebagai berikut :
1. Bubble sort
Bubble sort adalah suatu metode pengurutan yang membandingkan elemen yang sekarang dengan elemen berikutnya. Apabila elemen sekarang > elemen berikutnya, maka posisinya ditukar. Kalau tidak, tidak perlu ditukar. Diberi nama “Bubble” karena proses pengurutan secara berangsur-angsur bergerak/berpindah ke posisinya yang tepat, seperti gelembung yang keluar dari sebuah gelas bersoda.
Proses Bubble Sort :
Data paling akhir dibandingkan dengan data di depannya, jika ternyata lebih kecil atau besar maka tukar sesuai dengan ketentuan (descending atau ascending). Dan pengecekan yang sama dilakukan terhadap data yang selanjutnya sampai dengan data yang paling awal.

Gambar 6.1 Langkah 1 Bubble Sort
Gambar 6.2 Langkah 2 Bubble Sort

Gambar 6.3 Langkah 3 Bubble Sort
Algoritma Bubble Sort:
1. i = 0
2. Selama (i < N-1) kerjakan baris 3 sampai 7
3. j = N - 1
4. Selama (j >= i) kerjakan baris 5 sampai 7
5. Jika (Data[j-1] > Data[j]) maka tukar Data[j-1]dengan Data[j]
6. j = j - 1
7. i = i+ 1
Prosedur yang menggunakan metode gelembung:
void BubbleSort()
{
int i, j;
for(i=1; i<Max-1; i++)
for(j=Max-1; j>=i; j--)
if(Data[j-1] > Data[j])
Tukar(&Data[j-1], &Data[j]);
}
2. Selection Sort
Metode seleksi melakukan pengurutan dengan cara mencari dta yang terkecil kemudian menukarnya dengan data yang digunakan sebagai acuan atau sering dinamakan pivot. Selama proses, pembandingan dan pengubahan hanya dilakukan pada indeks pembanding saja,pertukaran data secara fisik terjadi pada akhir proses.proses pengurutan dengan metode seleksi dapat dijelaskan sebagai berikut:
· Langkah pertama dicari data terkecil dari data pertama sampai data terakhir. Kemudian data terkecil ditukar dengan data pertama. Dengan demikian, data pertama sekarang mempunyai nilai paling kecil dibanding data yang lain.
· Langkah kedua, data terkecil kita cari mulai data kedua sampai terakhir. Data terkecil yang kita peroleh ditukar dengan data kedua dan demikian seterusnya sampai semua elemen dalam keadaan terurutkan.
Gambar 6.4 Langkah Selection Sort
Algoritma seleksi dapat dituliskan sebagai berikut:
1. i = 0
2. Selama(i < N-1) kerjakan baris 3 sampai dengan 9
3. k = i
4. j = i + 1
5. Selama (j < N) kerjakan baris 6 dan 7
6. Jika (Data[k] > Data[j]) maka k = j
7. j = j + 1
8. Tukar Data[i] dengan Data[k]
9. i=i+1
Dibawah ini merupakan prosedur yang menggunakan metode seleksi:
void SelectionSort()
{
int i, j, k;
for(i=0; i< Max-1; i++)
{
k = i;
for(j=i+1; j<Max; j++)
if(Data[k] > Data[j])
f=j;
Tukar(&Data[i], &Data[k]);
}
}
3. Merger Sort
Algoritma Merge Sort ialah algoritma pengurutan yang berdasarkan pada strategi divide and conquer. Algoritma ini terdiri dari dua bagian utama, pembagian list yang diberikan untuk di-sort ke dalam beberapa sublist yang lebih kecil,dan sort (mengurutkan) dan merge (menggabungkan) sublist-sublist yang lebih kecil ke dalam list hasil yang sudah diurutkan. Pembagian bisa dikatakan cukup mudah karena sublist-sublist tersebut dibagi ke dalam dua sublist yang ukurannya adalah setengah dari ukuran semula. Hal ini terus diulang sampai sublist itu cukup kecil untuk di-sort secara efisien (umumnya telah terdiri dari satu atau dua elemen). Dalam langkah merge dua sublist disatukan kembali dan diurutkan pada saat yang sama. Algoritma untuk merge sort ialah sebagai berikut:
A. Untuk kasus n=1, maka table a sudah terurut sendiirinya (langkah solve)
B. Untuk kasus n>1, maka:
a. DEVIDE: bagi table a menjadi dua bagian, bagian kiri dan bagian kanan, masing-masing bagian berukuran n/2 elemen.
b. CONQUER: secara rekursif,terapkan algoritma D-dan-C pada masing-masing bagian.
c. MERGE: gabung hasil pengurutan kedua bagian sehingga diperoleh table a yang terurut.
Gambar 6.5 Contoh Merge Sort










Komentar
Posting Komentar